Совертков П.И.
РГПУ им. А.И.
Герцена,
г. Санкт-Петербург, Россия
Компьютерное
моделирование седловых поверхностей вращения с данным асимптотическим конусом
Изученные
в математике виды седловых поверхностей используются в строительстве и
архитектуре и, наоборот, строительство и архитектура сформулировали ряд заданий
для поиска седловых поверхностей с заданными свойствами (геометрическими,
жесткости, изгибаемости, прочности и сопротивляемости различным нагрузкам) [1].
В статье рассматриваются новые седловые поверхности вращения, асимптотически
приближающиеся к наперед заданным конусам. Первоначальный выбор прямых в
качестве будущих асимптот линий используется в дальнейшем для построения
поверхностей вращения с данной асимптотикой. Предложенный в данной статье метод
получения седловых поверхностей с помощью продолжения уравнения семейства
прямых по параметру ранее в литературе не отражен. Компьютерное моделирование
линий в качестве образующих для поверхности вращения седловых поверхностей
развивает операционное мышление участников разработки проектов, позволяет
выделить на поверхности различные линии.
Sovertkov P.I
HSPU
St.Peterburg, Russia
Computer simulation of saddle surfaces of rotation
with a given asymptotic cone
The types of saddle surfaces studied in mathematics
are used in construction and architecture, and, conversely, construction and
architecture have formulated a number of tasks to search for saddle surfaces
with specified properties (geometric, stiffness, bending, strength and
resistance to various loads) [1]. The article discusses new saddle surfaces of
rotation that asymptotically approach predetermined cones. The initial
selection of straight lines as future asymptote lines is then used to construct
surfaces of rotation with this asymptotics. The method proposed in this article
for obtaining saddle surfaces by means of a continuation of the equation of the
family of lines by parameter is not previously reflected in the literature.
Computer modeling of lines as forming surfaces of rotation and saddle surfaces
develops the operational thinking of project development participants, allows
you to identify various lines on the surface.
В настоящее время линии и поверхности в
статьях и пособиях часто изображаются с помощью программных продуктов GEOGEBRA, Mathcad
и т.д., математический аппарат которых использует основы проективной геометрии
и другие методы изображения начертательной геометрии и компьютерной графики. В
большинстве случаев эти рисунки формируют полное представление о поведении
линий и поверхностей и этого, оказывается, достаточно на уровне использования:
подставил – получил. Но существуют простой метод параллельного проектирования [2,
с. 271], а значит изображения пространственных точек на экране компьютера,
используя который, можно отразить особенности линии на поверхности. Простота
формул параллельного проектирования доступна школьнику и студенту. Если они на
экране компьютера получают рисунок, отличный от запланированного, то быстрее
происходит осмысление, в чем причина ошибки. Конечно, в этом случае происходит
большая затрата времени на написание программного кода и полученный рисунок не
всегда является таким наглядным. Большинство разработчиков компьютерных программ
скажет, что написанная программа с первого раза не запускается или изображает
что-то отличное от запланированного, но постепенно все мелкие погрешности
устраняются в процессе диалога программиста с компьютером. В процессе этого диалога
происходит понимание того, что на экране можно лучше изобразить некоторые
элементы поверхности. Например, штриховку линий или кусков поверхностей можно
выполнить с помощью программного кода под любой заказ рядом сидящего теоретика.
Меридианы и параллели поверхности вращения можно раздвигать, задавая
первоначально шаги между ними.
А самое главное в этом случае заключается
в том, что компьютерное моделирование оказывается перспективным элементом
формирования операционного мышления участника разработки проекта.
1. Седловая поверхность с чашей и острым рогом

Поверхность
вращения будем называть поверхностью с асимптотическим конусом, если существует
такой круговой конус, что при удалении точек поверхности в одном из направлений
оси конуса эти точки неограниченно близко приближаются к конусу. Простейшей
поверхностью с данным асимптотическим конусом является однополостный
гиперболоид. Однополостный гиперболоид вращения получается при вращении
гиперболы вокруг мнимой оси симметрии гиперболы. При вращении гиперболы вокруг
других прямых, можно получить седловые поверхности, отличные от гиперболоида.
На плоскости с
декартовой системой координат Оρz вертикальная ось z задана уравнением 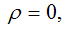 а наклонная прямая уравнением
а наклонная прямая уравнением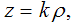 тогда объединение двух прямых определяется
уравнением
тогда объединение двух прямых определяется
уравнением 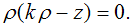 Включим полученное уравнение в семейство
уравнений
Включим полученное уравнение в семейство
уравнений 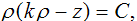 где С
– некоторая константа. Для
где С
– некоторая константа. Для 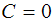 получим исходную пару пересекающихся прямых, а
для
получим исходную пару пересекающихся прямых, а
для 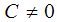 – семейство гипербол, асимптотами которых
являются пара исходных прямых. При
– семейство гипербол, асимптотами которых
являются пара исходных прямых. При 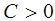 гипербола (рис. 1) имеет ветви γ1 и
γ2, а при
гипербола (рис. 1) имеет ветви γ1 и
γ2, а при 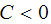 гипербола имеет ветви γ3 и γ4.
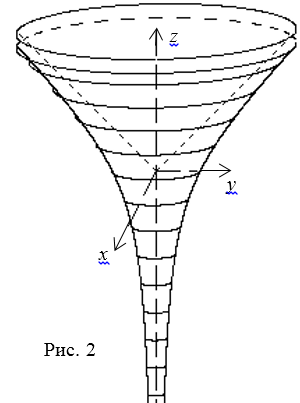
При повороте ветви γ1 гиперболы вокруг оси Oz, т.е. вокруг
асимптоты гиперболы получим поверхность вращения, отличную от поверхности
однополосного гиперболоида (рис. 2).
гипербола имеет ветви γ3 и γ4.
При повороте ветви γ1 гиперболы вокруг оси Oz, т.е. вокруг
асимптоты гиперболы получим поверхность вращения, отличную от поверхности
однополосного гиперболоида (рис. 2).
Уравнение ветви γ1 гиперболы: 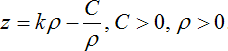 .
.
Программа построения рис. 1 на языке PascalABC:
Uses GraphABC; {вызов графического
редактора}
Var x0,y0,C,h,i:integer; {объявление
переменных}
k:
real; Begin
x0:=300; y0:=200; {точка отсчета, играющая
роль начала координат}
C:=400; k:=1; h:=100; {константы
данной задачи}
Line (x0-100,y0,x0+100,y0); Line
(x0,y0-200,x0,y0+200); {оси координат}
Line (x0-100,y0+round(k*100),x0+100,y0-round(k*100)); {наклонная прямая}
For i:=1 To 100*h Do Begin {цикл построения точек ветвей гиперболы }
PutPixel(x0+round(i/h),y0-round(-C/i*h+k*i/h),1);
PutPixel(x0-round(i/h),y0+round(-C/i*h+k*i/h),1);
PutPixel(x0+round(i/h),y0-round(C/i*h+k*i/h),1);
PutPixel(x0-round(i/h),y0+round(C/i*h+k*i/h),1); End; End.
Замечание. На некоторых участках линий
точки линии иногда изображаются разреженно, т.к. параметр цикла принимает
целочисленные значения. С целью получения непрерывной линии, т.е. получения
координат точек с дробными значениями в цикле вначале применяется умножение на
масштабную величину h, а затем деление на эту величину h.
Уравнение поверхности вращения 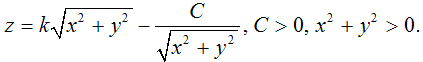
При удалении точек поверхности от начала координат в направлении  точки поверхности асимптотически приближаются к верхней полости конуса
точки поверхности асимптотически приближаются к верхней полости конуса 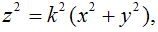 а при удалении точек поверхности в направлении
а при удалении точек поверхности в направлении 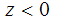 точки поверхности асимптотически
приближаются к отрицательному лучу оси z.
Можно сказать, что асимптотикой поверхности является конус с лучом, выходящим
из вершины конуса. Седловая поверхность содержит чашу и острый рог. Если
поверхность обрезать плоскостями, перпендикулярными оси z в положительном и
отрицательном направлениях, то поверхность можно использовать как капельницу.
Радиус нижнего сечения нужно определять в зависимости от плотности вытекающей
жидкости в сосуде, имеющем форму полученной поверхности.
точки поверхности асимптотически
приближаются к отрицательному лучу оси z.
Можно сказать, что асимптотикой поверхности является конус с лучом, выходящим
из вершины конуса. Седловая поверхность содержит чашу и острый рог. Если
поверхность обрезать плоскостями, перпендикулярными оси z в положительном и
отрицательном направлениях, то поверхность можно использовать как капельницу.
Радиус нижнего сечения нужно определять в зависимости от плотности вытекающей
жидкости в сосуде, имеющем форму полученной поверхности.
Для
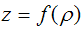
Если поверхность получена при вращении линии
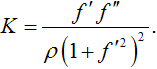
Для изучаемой поверхности вращения
гауссова кривизна равна 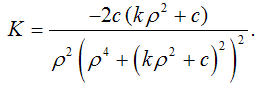
При 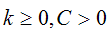 гауссова
кривизна поверхности является отрицательной, и поверхность является седловой.
гауссова
кривизна поверхности является отрицательной, и поверхность является седловой.
При
При параллельном проектировании координаты точки
изображения 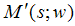 [2, с. 273] являются
линейными функциями координат точки – оригинала
[2, с. 273] являются
линейными функциями координат точки – оригинала 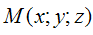 , т.е.
, т.е. 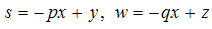 . где p и q - константы.
. где p и q - константы.
Программа построения рис. 2 на языке PascalABC:
Uses
GraphABC; {вызов графического редактора}
Var
x0,y0,C,h,i,j,d,m,s:integer; {объявление переменных}
k,z,p,q,r,x,y,a,u:
real; Begin
x0:=300; y0:=240;
C:=1000;k:=1; p:=-0.1; q:=-0.2; a:=Sqrt(C);
h:=200;
{высота верхнего основания конуса}
d:=20;{длина
шага в штриховке}
s:=20;{расстояние
между параллелями}
For i:=0 Tо 628 Do Begin {верхнее основание
конуса}
PutPixel(x0+round(p*h*cos(i/100)+h*sin(i/100)),y0-round(q*h*cos(i/100)+h),clBlue);End;
For i:=-h To h-10
Do Begin {боковые образующие поверхности}
r:=
(i+Sqrt(i*i+4*k*c))/2/k;
PutPixel(x0+round(r),y0-i,
clTeal); PutPixel(x0-round(r),y0-i, clTeal); End;
For i:=0 Tо 628 Do Begin {верхнее основание
поверхности}
x:=h*cos(i/100);
y:=h*sin(i/100); m:=trunc(i/d);
If x>0 Then
PutPixel(x0+round(p*x+y),y0-round(q*x+h-10),clGreen);
If ((x<0) And
(i-(m*d)<(d div 2))) Then
PutPixel(x0+round(p*x+y),y0-round(q*x+h-10),clGreen); End;
SetPenStyle(psDot);
Line
(x0,y0,x0+h,y0-round(k*h));Line (x0,y0,x0-h,y0-round(k*h)); {образующие конуса}
SetPenStyle(psDash);
Line
(x0,y0,x0+30,y0); Line (x0,y0-100,x0,y0+200); {оси координат}
Line(x0,y0,
x0+round(p*200), y0-round(q*200));
For j:=(-h div s)
Tо (h-20) div s Dо Begin {параллели поверхности}
For i:=-157 To 157
Dо Begin
z:=j*s;
r:=(z+Sqrt(z*z+4*c))/2;
PutPixel(x0+round(p*r*cos(i/100)+r*sin(i/100)),y0-round(q*r*cos(i/100)+z),1);
End; End; End.
2.
Седловая
поверхность с двумя различными чашами
Рассмотрим прямые,
заданные уравнениями 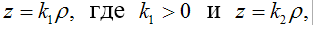 где
где 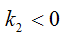 тогда объединение двух прямых определяется уравнением
тогда объединение двух прямых определяется уравнением 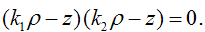 Включим полученное уравнение в семейство уравнений
Включим полученное уравнение в семейство уравнений 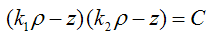
, где С – некоторая константа.
Для 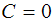 получим исходную пару
пересекающихся прямых,
получим исходную пару
пересекающихся прямых,
а для 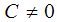
– семейство гипербол, асимптотами которых являются пара исходных прямых.
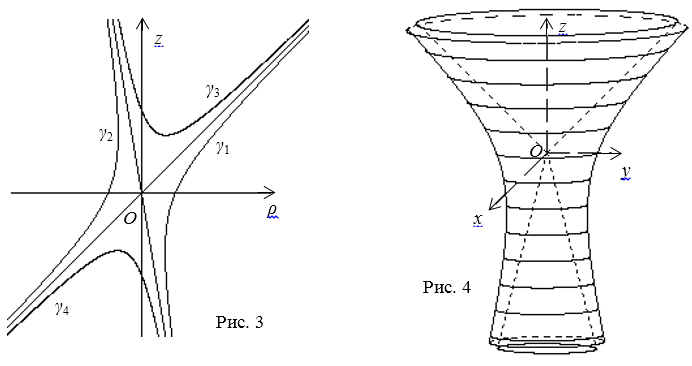
При 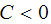 гипербола (рис. 3) имеет ветви γ1 и γ2, а при
гипербола (рис. 3) имеет ветви γ1 и γ2, а при 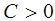 гипербола имеет
ветви γ3 и γ4. При повороте ветви γ1 гиперболы
вокруг оси Oz,
т.е. вокруг прямой, не являющейся осью симметрии гиперболы и не являющейся
асимптотой гиперболы, получим поверхность вращения, отличную от поверхности
однополосного гиперболоида (рис. 4).
гипербола имеет
ветви γ3 и γ4. При повороте ветви γ1 гиперболы
вокруг оси Oz,
т.е. вокруг прямой, не являющейся осью симметрии гиперболы и не являющейся
асимптотой гиперболы, получим поверхность вращения, отличную от поверхности
однополосного гиперболоида (рис. 4).
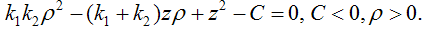
Уравнение поверхности вращения 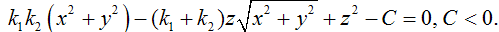
При удалении точек поверхности от начала координат в положительном
направлении оси z эти точки приближаются
асимптотически к конусу 3.
Седловая
поверхность, огибающая конус и цилиндр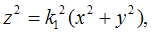 а при удалении в отрицательном направлении оси z, точки поверхности приближаются к конусу
а при удалении в отрицательном направлении оси z, точки поверхности приближаются к конусу 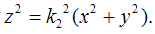 Если
Если 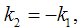 то поверхность превращается в однополостный гиперболоид вращения
то поверхность превращается в однополостный гиперболоид вращения 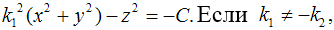 то седловая поверхность имеет две различные
чаши, приближающиеся к различным конусам.
то седловая поверхность имеет две различные
чаши, приближающиеся к различным конусам.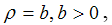 а наклонная прямая уравнением
а наклонная прямая уравнением 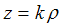 , тогда объединение двух прямых определяется уравнением
, тогда объединение двух прямых определяется уравнением 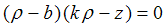 .. Включим полученное уравнение в семейство уравнений
.. Включим полученное уравнение в семейство уравнений 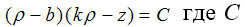 – некоторая константа. Для
– некоторая константа. Для 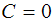 получим исходную пару пересекающихся прямых, а для
получим исходную пару пересекающихся прямых, а для 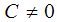 – семейство гипербол, асимптотами которых являются пара исходных прямых.
При повороте вокруг оси Oz ветви
гиперболы, заданной уравнением:
– семейство гипербол, асимптотами которых являются пара исходных прямых.
При повороте вокруг оси Oz ветви
гиперболы, заданной уравнением: 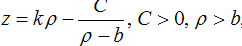 получим поверхность вращения (рис. 5) с уравнением
получим поверхность вращения (рис. 5) с уравнением 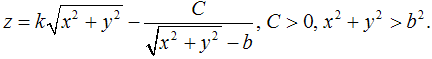
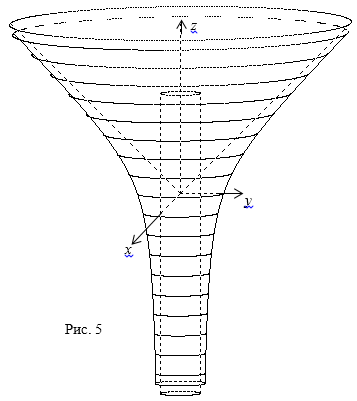
Поверхность
является седловой, имеет чашу и рог, асимптотически приближается к цилиндру или
конусу с общей осью, при удалении точек поверхности от начала координат (рис.
5).
Поверхность имеет форму лейки. В [1, с.
105] построена поверхность сопряжения соосных цилиндра и конуса, которая
используется для перехода с цилиндра на конус в компактной области.
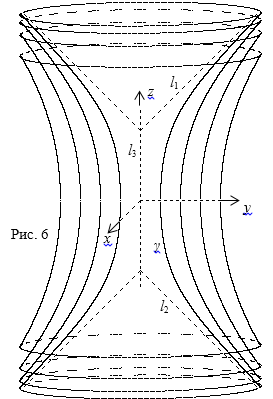
4.
Седловая
поверхность с раздвинутыми асимптотическими конусами
В плоскости Oρz рассмотрим прямые, заданные уравнениями 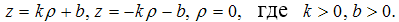 Объединение трех прямых задается уравнением
Объединение трех прямых задается уравнением 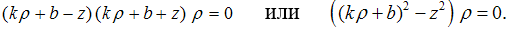 Включим полученное уравнение в семейство уравнений
Включим полученное уравнение в семейство уравнений 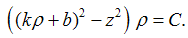 Выберем дугу γ линии третьего
порядка в области
Выберем дугу γ линии третьего
порядка в области 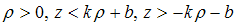 и повернем вокруг оси z. Для различных
положительных значений параметра С
получим семейство седловых поверхностей с раздвинутыми асимптотическими
конусами (рис. 6) . Поверхности задаются уравнением
и повернем вокруг оси z. Для различных
положительных значений параметра С
получим семейство седловых поверхностей с раздвинутыми асимптотическими
конусами (рис. 6) . Поверхности задаются уравнением 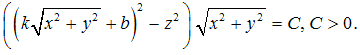
В заключении поясним общий метод
построения всех предложенных выше поверхностей. Для построения седловых
поверхностей, которые должны быть гладкими и неограниченными, выбирается
несколько прямых. Объединение прямых задается общим уравнением, в котором
произведение множителей приравнивается к нулю. Далее это уравнение включается в
семейство уравнений с параметром. Продолжение уравнение объединения прямых по
параметру обеспечивает асимптотику полученных кривых, т.е. приближение точек
кривых к данным прямым. На кривых выбираются дуги, обращенные выпуклостью к оси
вращения, чтобы получилась седловая поверхность. Этим методом можно получить
различные поверхности, отличные от приведенных в данной статье. 5.
Асимптотические
линии на поверхности капельнице
Уравнение
асимптотических линий поверхности, полученной при вращении линии 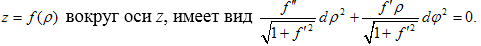

Получили два семейства асимптотических линий на поверхности вращения.
Одни линии закручиваются вправо, а другие линии влево. Асимптотические линии
расположены симметрично относительно меридианов на поверхности. Константа
интегрирования с означает, что линии
каждого семейства получаются поворотом
по поверхности вращения 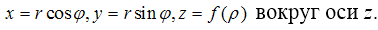
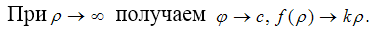 Это означает, что асимптотическая линия на
поверхности типа капельница стабилизирует свое направление в пространстве и
приближается к образующей асимптотического конуса. Кстати, образующая линия
асимптотического конуса является асимптотической линией на поверхности конуса.
Это означает, что асимптотическая линия на
поверхности типа капельница стабилизирует свое направление в пространстве и
приближается к образующей асимптотического конуса. Кстати, образующая линия
асимптотического конуса является асимптотической линией на поверхности конуса.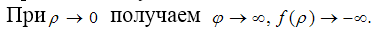 Это означает, что проекция точек
асимптотической линии на плоскость z = 0
Это означает, что проекция точек
асимптотической линии на плоскость z = 0