Совертков П.И.
РГПУ им. А.И.
Герцена,
г. Санкт-Петербург, Россия
Компьютерное моделирование банка задач на исследование функции с экстремумами в двух данных точках
Для
дистантной формы обучения предлагается метод автоматизации составления банка
задач и быстрой проверки решений учащихся по исследованию дробно рациональной
функции. Начальными параметрами функции являются наглядные геометрические
параметры - координаты двух точек экстремумов. Компьютерная программа написана
на языке PascalABC.
Sovertkov P.I.
HSPU
St. Peterburg, Russia
Computer
simulation of a task bank for investigating a function with extremes at two
data points
For the remote form of learning, a method is proposed to automate the compilation of a task bank and quickly verify students' decisions on the study of a fractional rational function. The initial parameters of the function are the visual geometric parameters - the coordinates of the two extremum points. The computer program is written in the PascalABC language.
Для индивидуальных занятий по математике во время дистантного обучения, а также для контрольно-измерительных материалов ЕГЭ по математике требуется большой набор заданий. Помочь преподавателю для составления условий задач и быстрой проверки может автоматизация этого процесса с помощью компьютерного моделирования.
Для проверки умения исследовать дробно рациональную функцию с двумя экстремумами разработана модель, в которой вводятся четыре параметра, т.е. координаты точек экстремумов. Компьютерная программа строит на экране график дробно рациональной функции, вертикальную и горизонтальную асимптоты, выводит на экран геометрические параметры графика: параметры наклонной асимптоты, параметр вертикальной асимптоты, удаление точек экстремума от вертикальной асимптоты. Компьютерная программа также выводит на экран аналитическое выражение функции используемого типа и конкретное выражение функции для введённых координат точек экстремумов.
Весь процесс составления условия задачи, изображения графика функции и автоматического вычисления аналитического выражения для функции с заданными параметрами сводится к вводу в компьютер четырёх чисел.
В течение небольшого промежутка времени преподаватель может составить десятки или сотню условий задач и быстро получить для дальнейшей проверки графики функций.
Ученик получает для исследования функции только аналитическое задание функции в виде формулы. В [2, с. 148-150] рассмотрена автоматизация составления банка задач для исследования функции
(1)
с
другими первоначальными параметрами:
k – угловой коэффициент наклонной асимптоты;
b – ордината точки пересечения наклонной асимптоты с
осью Oy;
a – абсцисса точки пересечения вертикальной асимптоты с
осью Ох;
q – расстояние от точки экстремума до вертикальной
асимптоты.
Используя четыре геометрических параметра можно быстро составить
большой банк заданий для индивидуальных заданий. Компьютерная программа [2, с. 151] строит
график функции и выводит на экран аналитическое выражение дробно рациональной
функции (1) для введённых конкретных значений параметров.
Точки
экстремумов и
расположены
симметрично относительно точки
пересечения
вертикальной и наклонной асимптот.
Введём
обозначения
Считая
заданными числами, найдём
(2)
Если
координаты точек экстремумов являются исходными параметрами, то функция
принимает вид
(3)
Формула
(3) задаёт гиперболу, имеющую две точки экстремумов и асимптоты, параметры
которых вычисляются по формулам (2).
После
введения конкретных значений для параметров можно строить график функции по формуле (3)
или по формуле (1), параметры a, q, k, b, для
которой предварительно вычисляются по формулам (2).
На
рис. 1 для точек экстремумов E1(-6; 6), E2(-2;-2)
построен график функции с геометрическими параметрами
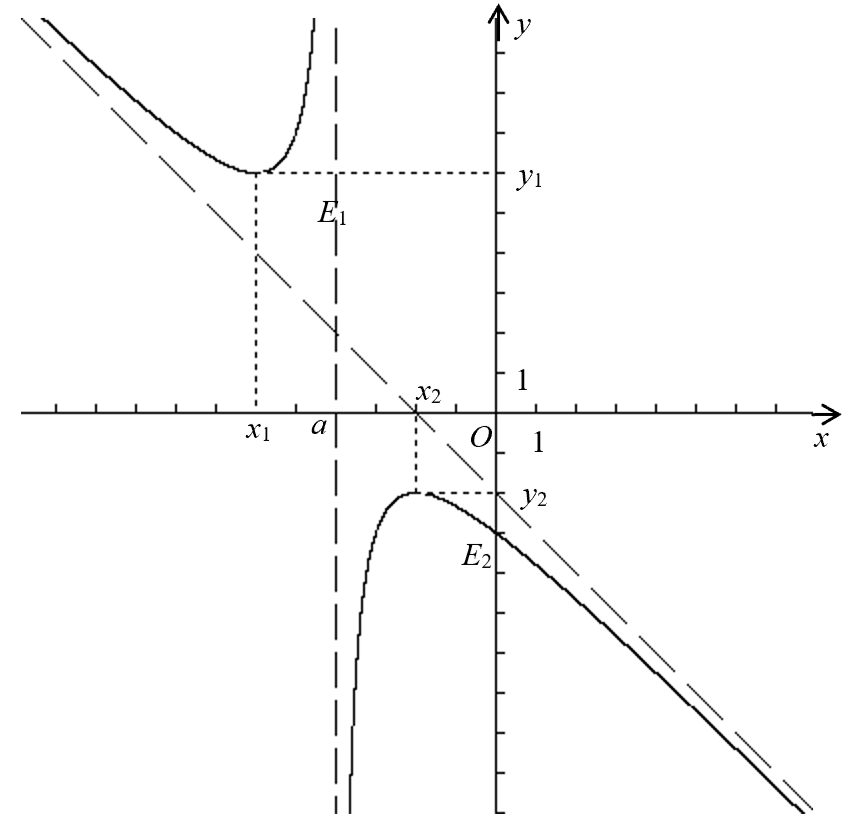
Рисунок 1
Компьютерная
программа построения графика с данными точками экстремумов написана на языке Pascal
ABC [1]. Ею может воспользоваться учитель в любой школе.
Uses
GraphABC;
Var
x0,y0,x1,y1,x2,y2,i,x,m,n,h:Integer; a,b,k,q,y: real; Begin
x0:=200;
y0:=200; m:=20; n:=9; x1:=-4; y1:=-6; x2:=-2; y2:=2; h:=1000;
{m-масштаб,
n-число меток на осях, h-увеличение числа точек на графике}
Line
(x0-n*m,y0,x0+n*m,y0); Line (x0,y0-n*m,x0,y0+n*m); {оси координат}
a:=(x1+x2)/2;
q:=(x2-x1)/2; k:=(y2-y1)/(x2-x1)/2; {геометрические параметры}
b:=((x2-3*x1)*y2-(x1-3*x2)*y1)/(x2-x1)/4;
For
x:=round(a*h+1) To n*h Do Begin {точки графика правее вертикали}
y:=((y2-y1)*x*x/h/h+2*(y1*x2-y2*x1)*x/h+y2*x1*x1-y1*x2*x2)/(x2-x1)/(x/h-a)/2;
PutPixel
(x0+round(x*m/h),y0-round(y*m),1); End;
For
x:=-n*h To round(a*h-1) Do Begin {точки графика левее вертикали}
y:=((y2-y1)*x*x/h/h+2*(y1*x2-y2*x1)*x/h+y2*x1*x1-y1*x2*x2)/(x2-x1)/(x/h-a)/2;
PutPixel (x0+round(x*m/h),y0-round(y*m),1);
End;
For
i:=-n To n Do Begin {расстановка меток на осях координат}
Line
(x0+i*m,y0,x0+i*m, y0-5); Line (x0,y0+i*m,x0+5, y0+i*m); End;
SetPenStyle(psDash);
{стиль линии для асимптот}
Line(x0+round(a*m),y0-n*m,x0+round(a*m),y0+n*m);
{вертикальная асимптота}
Line(x0-n*m,y0-round((-k*n+b)*m),x0+n*m,y0-round((k*n+b)*m));
{наклонная}
SetPenStyle(psDot);
{стиль линии для проекций точек экстремумов}
Line
(x0+round(x1*m),y0-round(y1*m),x0+round(x1*m),y0);{проекция Е1 на Ох}
Line
(x0+round(x2*m),y0-round(y2*m),x0+round(x2*m),y0); {проекция Е2 на Ох}
Line
(x0+round(x1*m),y0-round(y1*m),x0,y0-round(y1*m)); {проекция Е1 на Оу}
Line
(x0+round(x2*m),y0-round(y2*m),x0,y0-round(y2*m)); {проекция Е2 на Оy}
Write
('Экстремумы Е1(',x1,';',y1, '), E2(',x2,';',y2,').'); Writeln;
Writeln
('Геометрические параметры: b=',b:4:2,'; k=',k:4:2,'; q=',q,'; a=',a);
Writeln
('Формула: y=(kxx+(b-a*k)*x+kqq-ab)/(x-a)');{вид функции}
Write
('Функция: y=(',k:4:2,'*x*x+(',b-a*k:4:2,')*x+',k*q*q-a*b:4:2,')/(x-(',a,'))');
End.
Рассмотренное
моделирование имеет важное значение для сглаживания угла [1, c. 282-286; 3; 4, c.
28-31]. Практические задачи по сглаживанию угла возникают при конструировании
фюзеляжей самолётов, корпусов кораблей и других механизмов.
Применим метод продолжения по параметру, изложенный в [3], чтобы получить формулу (1).
Пусть
вертикальная асимптота задана уравнением а
наклонная асимптота уравнением
тогда
объединение этих асимптот задано уравнением
. Включим уравнение пары асимптот в семейство
уравнений
где C - произвольная константа. Выражая
переменную у, получим
Выбирая
константу в виде
чтобы
параметры имели геометрическое значение, получаем формулу (1).
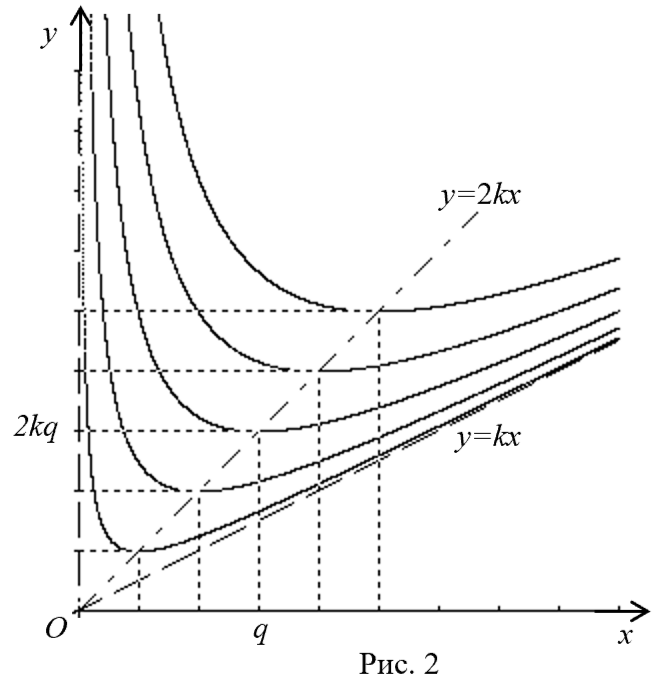
На
рис. 2 построен угол с вершиной О, сторонами которого являются ось
ординат и наклонная асимптота Для данного угла построено несколько гипербол,
ветви которых асимптотически приближаются к сторонам угла. Для произвольного
значения q построено несколько точек E(q; 2kq),
которые являются точками экстремума графика функции внутри данного угла.
Отметим, что точки экстремумов расположены на прямой с уравнением
Рассмотрим
важное замечание. В школьном и вузовском курсах математики сообщается, что
функциональную зависимость одной переменной от другой переменной можно задавать
различными способами и в дальнейшем все функции в математике представляются в
виде Поэтому переменной х соответствует
единственное значение у. Графики с горизонтальной асимптотой почти
отсутствуют и, тем более, отсутствуют графики, на которых переменной х
соответствует несколько значений переменной у.
Для восполнения
этого недочёта предлагается исследовать функции вида .
Компьютерная
программа для построения нового типа функций:
Uses GraphABC; Var x0,y0,k,b,a,q,m,i,y,h,n:Integer; x:real; Begin
x0:=300; y0:=240; k:=-2; b:=-4; a:=-3;q:=1; m:=20;n:=12; h:=1000;
Line (-n*m+x0,y0,n*m+x0,y0); {ось Ох}Line (x0,-n*m+y0,x0,n*m+y0); {ось
Оу}
SetPenStyle(psDash); {стиль штриховой линии для асимптот}
Line
(-n*m+x0,-a*m+y0,n*m+x0,-a*m+y0); {горизонтальная асимптота}
Line ((-k*n+b)*m+x0,n*m+y0,(k*n+b)*m+x0,-n*m+y0); {наклонная}
For i:=-n To n Do Begin {цикл построения меток на осях}
Line (i*m+x0,y0,i*m+x0,-5+y0); Line (x0,i*m+y0,-5+x0,i*m+y0); End;
For y:=-n*100 To a*100-1 Do Begin
{точки графика ниже горизонтальной асимптоты}
x:=(k*y*y/10000+(b-a*k)*y/100+k*q*q-a*b)/(y/100-a);
PutPixel(trunc(x*m)+x0, -Trunc(y*m/100)+y0,clBlack); End;
For y:=a*100+1 To n*100 Do Begin
{точки графика выше горизонтальной асимптоты}
x:=(k*y*y/10000+(b-a*k)*y/100+k*q*q-a*b)/(y/100-a);
PutPixel(trunc(x*m)+x0, -Trunc(y*m/100)+y0,clBlack); End;
SetPenStyle(psDot); {стиль пуктирной линии }
Line ((k*a+b-2*k*q)*m+x0,-(a-q)*m+y0,(k*a+b-2*k*q)*m+x0,y0);
{проекция Е2 на Ох}
Line ((k*a+b-2*k*q)*m+x0,-(a-q)*m+y0,x0,-(a-q)*m+y0); {проекция Е2 на
Оy}
Line ((k*a+b+2*k*q)*m+x0,-(a+q)*m+y0,(k*a+b+2*k*q)*m+x0,y0);
{проекция Е1 на Ох}
Line ((k*a+b+2*k*q)*m+x0,-(a+q)*m+y0,x0,-(a+q)*m+y0); {проекция Е1 на
Оy}
Write ('Экстремумы E1(',k*a+b+2*k*q,';',a+q,'), Е2(',k*a+b-2*k*q,';',a-q,
'), .'); Writeln;
Writeln ('Геометрические параметры: b=',b,'; k=',k,'; q=',q,'; a=',a);
Writeln ('Формула: x=(kyy+(b-a*k)*y+kqq-ab)/(y-a)');{вид функции}
Write ('Функция: x=(',k,'*y*y+(',b-a*k,')*y+',k*q*q-a*b,')/(y-(',a,'))');
end.
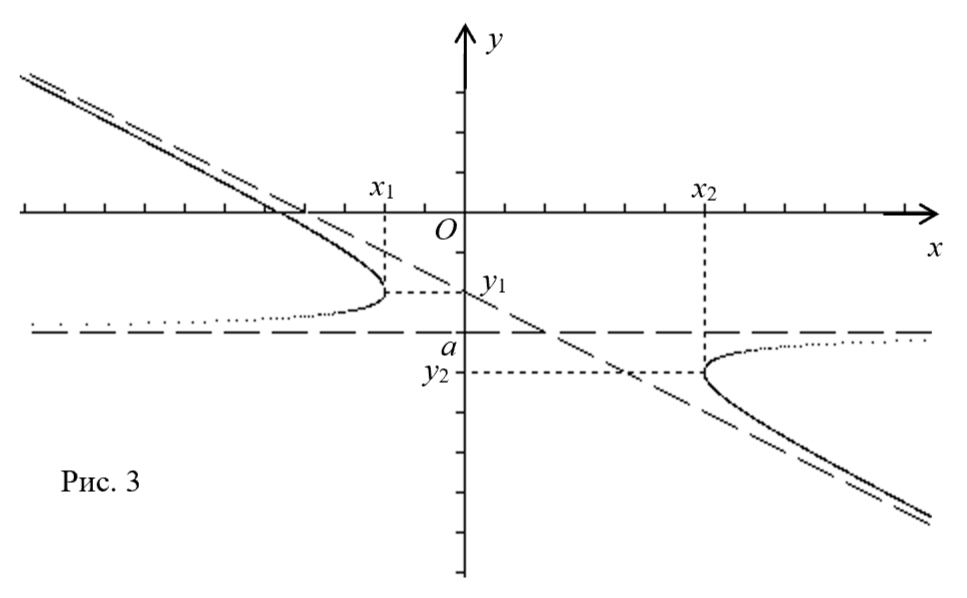
Для рис. 3 компьютерная программа построила
график функции и сообщила следующую информацию.
Экстремумы E1(-2;-2), Е2(6;-4) .
Геометрические параметры: b= -4; k= -2; q=1; a=
-3
Формула: x=k*y*y+(b-a*k)*y+k*q*q-a*b)/(y-a).
Функция:
Литература:
1. Совертков П.И.
Занимательное компьютерное моделирование в элементарной математике. М.: Гелиос
АРВ, 2004.
2. Совертков П.И.
Компьютерное моделирование. СПб: Лань, 2023.
3. Совертков П.И.
Семейство огибающих линий // Математика для школьников, 2024, № 4.
Фокс А., Пратт М. Вычислительная геометрия. М.:Мир, 1982.